 |
 |
|||||||||||
|
|
|||||||||||
|
Study of letter serial correlation (LSC) in some English, Hebrew, Aramaic, and Russian texts4.Discussion and interpretation of experimental results
|
Title |
Language |
O or T |
n of minimum |
n of Upcross |
Comment |
Max. chunk's size |
Genesis |
Hebrew |
O |
22 |
120 |
Entire text |
10000 |
Genesis |
English |
T |
30 |
400 |
Entire text |
10000 |
Genesis |
English |
T |
30 |
200 |
Entire text, no vowels |
10000 |
Genesis |
Aramaic |
T |
20 |
120 |
Entire text |
10000 |
Genesis |
Hebrew |
O |
30 |
120 |
Samaritan vesion |
10000 |
Torah |
Hebrew |
O |
20 |
120 |
Entire text |
1000000 |
Torah |
Aramaic |
T |
20 |
120 |
Entire text |
10000 |
Mishna |
Hebrew |
O |
20 |
85 |
Entire text |
10000 |
Talmud |
Heb+Aram. |
O |
20 |
70 |
Entire text |
3000000 |
War and Peace |
Hebrew |
T |
20 |
150 |
Initial part, 78064 letters |
10000 |
War and Peace |
English |
T |
70 |
700 |
Entire text |
1000000 |
War and Peace |
English |
T |
35 |
200 |
Entire text, no vowels |
500000 |
War and Peace |
English |
T |
30 |
150 |
Entire tetxt, no conson. |
10000 |
War and Peace |
English |
T |
70 |
600 |
Initial part, 107100 letters |
10000 |
War and Peace |
English |
T |
30 |
250 |
Same as above, no vow |
10000 |
War and Peace |
English |
T |
10 |
400 |
Same as above, no cons. |
10000 |
Moby Dick |
English |
O |
50 |
600 |
Entire text |
300000 |
Moby Dick |
English |
O |
30 |
300 |
Entire text, no vowels |
200000 |
Moby Dick |
English |
O |
10 |
85 |
Entire text, no cons. |
10000 |
UN Sea trade conv. |
English |
O |
85 |
550 |
Entire text |
10000 |
UN Sea trade conv. |
English |
O |
75 |
150 |
Entire text, no vowels |
10000 |
UN Sea trade conv. |
English |
O |
20 |
150 |
Entire text, no cons |
10000 |
Macbeth |
English |
O |
30 |
150 |
Entire text |
10000 |
Macbeth |
English |
O |
20 |
85 |
Entire text, no vowels |
10000 |
Macbeth |
English |
O |
10 |
150 |
Entire text, no cons. |
10000 |
Hiawatha |
English |
O |
30 |
400 |
Entire text. |
10000 |
Hiawatha |
English |
O |
20 |
150 |
Entire text, no vowels |
10000 |
Hiawatha |
English |
O |
10 |
500 |
Entire text, no cons. |
10000 |
Short stories1 |
English |
P |
70 |
350 |
Entire text, |
10000 |
Short stories 1 |
English |
P |
30 |
150 |
Entire text, no vowels |
10000 |
Short stories 1 |
English |
P |
10 |
150 |
Entire text, no cons. |
10000 |
Short stories 2 |
Russian |
P |
40 |
250 |
Entire text |
10000 |
Short stories 2 |
Russian |
P |
25 |
150 |
Entire text, no vowels |
10000 |
Newspaper |
Russian |
O |
40 |
350 |
Entire text, |
10000 |
Newspaper |
Russian |
O |
25 |
150 |
Entire text, no vowels |
10000 |
The third from left column in Table 5 indicates whether the text is in its original language (as signified by letter O) or it is a translation (indicated by letter T). Details in regard to original languages of the translated texts can be viewed in Table 4. The values of chunk's size - nm - where the Primary Minimum Points were observed are given in the fourth from left column in Table 5. The rightmost column in Table 5 lists the maximum size of chunks used in particular texts. The minimum size of a chunk was 1 for all texts.
Besides the data given in Table 5, additional data in regard to the locations of the Primary Minimum Points were shown and partially discussed earlier, for the text of War and Peace divided into 23 equals parts, as well as for texts of variable length, created both by adding identical segments of text and by adding its sequential segments.
Besides Primary Minimum Points, which are present in all texts, in some texts also secondary minima appear which are listed in Table 6. The secondary minimum points listed in Table 6 are those remaining on the experimental curves after artifacts have been filtered out.
Table 6. Secondary minima, secondary upcross points, peak points, and "degrees of randomness"
No |
Title |
O or T |
Language |
sec. min |
sec. cross |
n of peak |
Dr |
Comment |
1 |
Genesis |
O |
Hebrew |
none | none | 7000 | 0.2 |
Entire text |
2 |
Genesis |
T |
English |
none | 600 |
3000 | 0.3 |
Entire text |
3 |
Genesis |
T |
English |
none | 350 |
7000 | 0.41 |
Entire text, no vowels |
4 |
Genesis |
T |
Aramaic |
none | none | n/observ. | 0.194 |
Entire text |
5 |
Genesis |
O |
Hebrew |
none | none | n/observ. | 0.243 |
Samaritan version |
6 |
Torah |
O |
Hebrew |
none | none | 50000 | 0.123 |
Entire text |
7 |
Torah |
T |
Aramaic |
none | none | n/observ | 0.129 |
Entire text |
8 |
Mishna |
O |
Hebrew |
none | none | n/observ. | 0.25 |
Entire text |
9 |
Talmud |
O |
Heb+Aram. |
none | none | 1000000 | 0.334 |
Entire text |
10 |
War and Peace |
T |
Hebrew |
none | none | n/observ. | 0.41 |
Initial part, 78064 letters |
11 |
War and Peace |
T |
English |
none | none | 500000 | 0.68 |
Entire text |
12 |
War and Peace |
T |
English |
none | none | 200000 | 0.69 |
Entire text, no vowels |
13 |
War and Peace |
T |
English |
none | none | n/observ. | 0.42 |
Entire text, no conson. |
14 |
War and Peace |
T |
English |
70 |
none | 5000 | 0.76 |
Initial part, 107100 letters |
15 |
War and Peace |
T |
English |
100 |
none | 5000 | 0.69 |
Same as above, no vow |
16 |
War and Peace |
T |
English |
50 |
none | 7000 | 0.42 |
Same as above, no cons. |
17 |
Moby Dick |
O |
English |
none | none | 200000 | 0.707 |
Entire text |
18 |
Moby Dick |
O |
English |
none | none | 100000 | 0.595 |
Entire text, no vowels |
19 |
Moby Dick |
O |
English |
30 |
none | 7000 | 0.572 |
Entire text, no cons. |
20 |
UN Sea trade conv. |
O |
English |
none | none | n/observ. | 0.416 |
Entire text |
21 |
UN Sea trade conv. |
O |
English |
none | none | n/observ. | 0.219 |
Entire text, no vowels |
22 |
UN Sea trade conv. |
O |
English |
100 |
none | 5000 | 0.297 |
Entire text, no cons |
23 |
Macbeth |
O |
English |
none | none | n/observ. | 0.61 |
Entire text |
24 |
Macbeth |
O |
English |
20 |
none | 7000 | 0.63 |
Entire text, no vowels |
25 |
Macbeth |
O |
English |
none | none | 3000 | 0.56 |
Entire text, no cons. |
26 |
Hiawatha |
O |
English |
1000 |
40 |
n/observ. | 0.674 |
Entire text. |
27 |
Hiawatha |
O |
English |
70 |
none | 5000 | 0.557 |
Entire text, no vowels |
28 |
Hiawatha |
O |
English |
70 |
none | n/observ. | 0.325 |
Entire text, no cons. |
29 |
Short stories 1 |
P |
English |
none | none | n/observ. | 0.472 |
Entire text, |
30 |
Short stories 1 |
P |
English |
none | none | n/observ. | 0.595 |
Entire text, no vowels |
31 |
Short stories 1 |
P |
English |
none | none | n/observ. | 0.544 |
Entire text, no cons. |
32 |
Short stories 2 |
P |
Russian |
none | 250 |
n/observ. | 0.319 | Entire text |
33 |
Short stories 2 |
P |
Russian |
none | none | n/observ. | 0.517 |
Entire text, no vowels |
34 |
Newspaper |
O |
Russian |
none | none | n/observ. | 0.632 |
Entire text, |
35 |
Newspaper |
O |
Russian |
none | none | n/observ. | 0.577 |
Entire text, no vowels |
Notations in Table 6 are the same as in Table 5. The values of n where secondary minima appear are shown in the fifth column from left.
The values of n where the upcross points were observed are gathered in Table 5. In some texts secondary upcross points appeared. Their locations are indicated in Table 6, in sixth column from left. These upcross points are those remaining on the curves after artifacts have been filtered out.
d. Peak points
Peak points were observed not on all curves, and therefore they are indicated in Table 6, where B-type points are gathered, rather than in Table 5 which contains the data for A-type points. The peaks listed in Table 6 are those which remained on the curves after artifacts had been filtered out.
e. Degree of randomness.
Additionally to the lists of the characteristic points discovered experimentally on the graphs for Letter Serial Correlation sums, Table 6 contains also the list of values of what we introduced as Degree of randomness, which is an arbitrarily constructed, calculated rather than directly observed coefficient Dr , reflecting in a certain imprecise way the similarity between a studied text and a fully randomized version. We calculated all values of that coefficient, gathered in Table 6, limiting the maximum chunks' size to 10000 letters. One reason for that restriction was the fact that a considerable portion of the studied texts had the total size not exceeding about 150000 letters, and some of them even considerably less. Naturally, in such relatively short texts, the size of chunks exceeding n=10000 seemed to be uselessly large. On the other hand, in some, longer texts, the maximum size of chunks was well above 10000 letters. However, to make possible a comparison of Dr values for all texts, we calculated Dr for those longer texts also limiting the chunk's maximum size to 10000 letters. Another reason for the above limitation on the maximum chunk' size was that for n>10000 the measured sum often exceeded tens of times the expected sum. At such ratios of Sm/Se, the concept of degree of randomness as represented by coefficient Dr becomes uncertain and hardly can be reasonably interpreted.
5. Interpretation of experimental data
In regard to the interpretation of downcross points, we have to answer three question, to wit:
1) Why in all texts, without a single exception, at chunk's size n=1, and in some texts also at n=2, the measured sum Sm is invariably larger than the expected sum Se (the latter is calculated based on the assumption of the text being randomized by permutations)?
2) Why at values of chunk's size, n, exceeding the above numbers (either n=1 or n=2) the measured sum Sm invariably becomes smaller than the expected sum Se?
3) Why in all Hebrew and Aramaic texts, in all Russian all-letter texts, and in the original English texts stripped of vowels or of consonants, the downcross point is between n=1 and n=2, while in all original all-letter English texts and in Russian texts stripped of vowels, the downcross point is between n=2 and n=3?
Here are the answers we offer for the above three questions.
1) The first question seems to be the easiest to answer.
Indeed, if n=1, it means that each chunk contains only 1 letter.
First consider a randomized text. Choose an arbitrary chink No i. The probability of any letter x to be found in that chunk equals px,i =Mx/L where Mx is the number of occurrences of letter x in the entire text and L is the total length of the text. If, in a randomized text, chunk No i does indeed contain letter x, it means that the probability to find the same letter x in the adjacent chunk No (i+1) is px,i+1=(Mx-1)/(L-1), which is very close to the value of p for chunk No i. and is similar for any other letter of the alphabet.
In a real meaningful text the situation is different. In real meaningful texts the appearance of the same letter twice in a row is rare, and this is generally true for most languages, even if not to the same extent (for example double l and double c happen more often in Italian than in English or Russian, and both double vowels and double consonants happen much more often in Finnish/Estonian than in English or Russian, etc). Hence, in most meaningful texts the probability of the same letter to appear twice in a row is less than the probability that two consecutive letters are different. Therefore in most real meaningful texts (more specifically in Hebrew, English, and Russian) the appearance of the same letter in two adjacent chunks whose sizes are 1 is naturally less frequent, on the average, than in a randomized text. If any two adjacent chunks of size 1 contain the same letter, the corresponding term in the LSC sum for these two chunks is zero. Then, on the average, in a randomized text there are more pairs of adjacent chunks of size 1, for which the corresponding term in the sum Sm equals zero. Overall, when chunk's size is 1, the LSC sum for a randomized text is naturally smaller than for a meaningful text. Hence, we ascribe the appearance of the DCP to P-factor.
To reiterate the above consideration, if any letter appears in the text twice in a row (such as cc, ll. uu, oo, etc) then for small chunks it leads to the decrease of the LSC sum. This factor is especially felt at n=1. The more of neighboring chunks of n=1 contain identical letters, the more terms in the LSC sum have zero value. As n grows above n=1 the role of P-factor rapidly diminishes. However, some influence of the frequency of occurrence of two identical letters in a row can be well felt at least until n crosses the value of the Primary Minimum Point.
The above explanation is well in agreement with the shift of the Downcross Point observed when texts are stripped of either vowels or consonants. For example, in English texts, removing all vowels results in the shift of the DCP from being between n=2 and n=3, to being between n=1 and n=2. This phenomenon reflects the different frequencies of doubled consonants vs doubled vowels in English texts. In those texts, double consonants (such as rr , ll etc) happen slightly more often than double vowels. In the all-letter English text the double consonants are "diluted" by vowels. When all vowels are removed, the concentration of pairs of consecutive identical letters in the text slightly increases, thus increasing the number of zero-value terms in the LSC sum, so that the latter slightly decreases, and the DCP shifts toward smaller n. In some other texts (for example, in the Russian texts explored so far) the removal of vowels causes the opposite effect, namely the shift of DCP from being between n=1 and n=2 to being between n=2 and n=3. This effect is the result of the larger frequency of pairs of identical vowels in those texts as compared to pairs of identical consonants.
As the chunk's size grows, the probability to encounter identical letters in any two adjacent chunks changes little if it is a randomized text, but increases measurably for meaningful texts, thus decreasing Sm for the latter.
2) The second question requires a little more complex answer.
In Part 3 of this report, examples of graphs were shown for Letter Serial Correlation density. This quantity has been found to decrease rather uniformly as the chunk's size grows, and this behavior is common for all texts without a single exception (see, for example, Figs 24-25). The LSC density was defined as the LSC sum per one letter in a chunk. In other words, as the chunk's size increases, the contribution of each individual letter to the Letter Serial Correlation sum always decreases.
Now let us return to the interpretation of the experimentally observed shape of the Sm vs n curve at relatively small n.
The experimental evidence shows quite decisively that at relatively small chunk's sizes, not exceeding by much n=1, the decreasing contribution of individual letters to the LSC sum is at least one of the reasons for the decrease of the LSC sum.
Of course, an explanation is still needed as to why the contribution of individual letters to the LSC sum decreases as n grows above n=1 in some texts or above n=2 in some other texts.
To answer that question, let us consider the following notions.
(i) The more varied is the letter composition of chunks, the larger is the SLC sum. The decrease of a sum means that the letter compositions of neighboring chunks has become more uniform. It is natural, since when chunks are very small, such that n<z where z is the number of letters in the alphabet, not every letter of the alphabet can find a space for itself in a chunk. In such a situation, there is a larger chance that those few letters lucky enough to be found in each chunk, will vary from chunk to chunk. As the size of the chunk increases, but is still less than z, it encompasses more letters, thereby enhancing the opportunity for more of identical letters to appear in a neighboring chunks. This effect must take place in both randomized and meaningful texts. However, in randomized texts the described effect is mitigated because of the chaoticity of letters distribution over the text. As the chunk's size increases, the letter composition of chunks becomes more uniform, as all additional letters appearing in the increased chunk must come from the same constrained pool (recall our example with a text where word apple was repeated many times). As more identical letters are added to chunks, individual contributions of each of them must decrease (as the appearance of any two identical letters in neighboring chunks means a zero term in the sum). (ii)
Hence, as the chunk's size increases (up to a certain extent - see an elaboration in the next section) both the expected and the measured sum decrease. The measured sum decreases faster because the effect determined by the chance of identical letters to appear twice in a row, while changing little for randomized texts, weakens measurably for the meaningful text. The result is that the curve for the measured sum, which starts, at n=1, above that for the expected sum, soon drops below the curve for the expected sum.
3) The third question requires an even more complex answer. To approach a possible answer to that question, let us view graphs in Figs. 44 through 47. These Figs show examples of zoomed-in graphs of the ratio R=Sm /Se for an English (The Song of Hiawatha) and a Russian (a Moscow newspaper) texts.
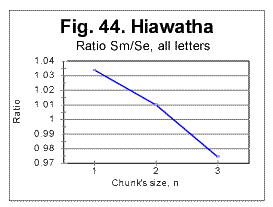
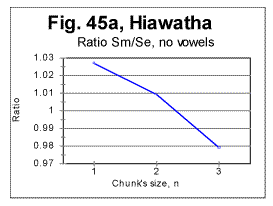



In all these graphs, the location of the downcross point (DCP) is where the curve crosses the level of R=1. The downcross point for the all-letter text of the Song of Hiawatha (Fig. 44) is between n=2 and n=3 which is typical of all original English texts. In the same text stripped of vowels, the DCP remains also between n=2 and n=3 (Fig. 45a). From Figs 44 and 45a it is evident that the said location of the downcross point is ensured by the proper slope of the R vs n curve between n=1 and n=2. Stripping the text in question of vowels did not substantially alter that slope, so the DCP is at about the same n for both the all-letter and no-vowels texts.
The described independence of the location of DCP in the Song of Hiawatha of the presence or absence of vowels in the text can be understood if we note that the text of that poem contains a multitude of rather long words from American Indian language, specifically various names of Gods, people, places, etc. This alien vocabulary element changes the ratio of the number of pairs of identical consecutive consonants to that of vowels, and thus depresses the shift of DCP toward lower n, which is observed in most other English texts.
Stripping the text of consonants (Fig. 45b) has a much stronger effect, making steeper the slope of the R vs n curve between n=1 and n=2, and the DCP now is found between n=1 and n=2, which is what has been observed also for all Hebrew texts. This can be explained by noting that stripping the text from consonants makes words practically unrecognizable, so the "alien" vocabulary element loses its distinction from any other, indigenous English words, and the P-factor is again in force, as it is in most other English texts.
Figs 46 and 47 show the behavior of ratio R=Sm/Se for a Russian text, for both the all-letter version and a version stripped of vowels. Here the picture is in a certain sense opposite to that with the Song of Hiawatha. In the all-letter Russian text the DCP is between n=1 and n=2 (like it is in all Hebrew texts). In the no-vowels Russian text, the slope of R vs n curve between n=1 and n=2 is less steep than in the all-letter text, and the downcross point shifts to a location between n=2 and n=3 (which is where it is in the all-letter original English texts). As it was mentioned before, the shift of DCP toward larger n in Russian texts can be explained by the inverse ratio of the number of occurrences of pairs of identical consonants to that of vowels, compared to regular English texts.
One more consideration seems to be relevant to the explanation of the DCP locations. Let us notice that the drop of the measured sum betwen n=1 and n=2 is affected also by such accidental factor as the total length of a text being either an even or an odd number. If L is an even number, then for n=2 no residual chunk is created whose length would be less than it is for all other chunks. Therefore in the case of an even L, no text's truncation takes place at n=2. If though L is an odd number, then for n=2 the text must be truncated, by casting off the residual incomplete chunk, as k=L/2 is in this case not an integer. Then, for n=2 the total length of the tested text is L*<L. This shrinkage of the text's length at n=2 results in a local decrease of the SLC sums at n=2 as compared with the case when L is an even number and L*=L. The decrease of the LSC sum at n=2 causes the Sm vs n curve to drop steeper between n=1 and n=2 than it would if no truncation took place, i.e. if L were an even number. However the picture is a little more complex. If L is an odd number, L* is less than L just by 1 letter. This difference may be suffucient to cause discernable increase in the curve's steepness, but the steepness increase in question depends also on the magnitude of L. If the total length of the text is, say, L=200000 the increase of the curve's steepness because of the loss of 1 letter will be much less pronounced than if L=50000.
Hence, the variations in the location of the downcross point are determined by the superimposition of several factors, to wit: a) The main factor affecting the location of DCP seems to be the frequency of occurrences of pairs of identical consecutive letters in a text (P-factor). b) Another factor seems to be just the number of letters in the alphabet (A-factor). The shorter is the alphabet, the stronger is the tendency for the downcross point to happen closer to n=1, i.e. usually between n=1 and n=2. This factor seems to be dominant in Hebrew texts as well as in English texts stripped of consonants, and sometimes also in English texts stripped of vowels. To the contrary, the longer an alphabet is, the stronger is the tendency of the downcross point to shift toward larger n, usually winding up between n=2 and n=3. Another effect is superimposed, namely: c) The accident of the text's total length being either an even or an odd number. L being an odd number creates a tendency for the downcross location to shift slightly away from n=1, often resulting in it being between n=2 and n=3. This effect of an odd L is also dependent on one more factor: d) The total length of a text. The shorter is the text whose length is an odd number, the stronger is felt the effect of a text truncation. Overall, shorter alphabet, odd value of L and shorter lengths L (in the case of an odd L), favor the downcross point to happen between n=1and n=2, while longer alphabet, even number for L, and, (if L is an odd number), longer L, favor the downcross point to happen between n=2 and n=3. The observed locations of the downcross points are products of interaction of the listed main factors, among which P-factor is probably the most influential. This does not exclude a possibility that some additional, probably subtler factors may affect the DCP as well. Among such additional factors may be, for example, the particular contents of a text (C-factor) the size of the vocabulary (V-factor), or the size of the "unit of contents" (G-factor).
After the artifacts caused by the text's truncation have been filtered out, there remains at least one distinctive minimum on every graph showing the measured sum Sm as a function of chunk's size n (see, for example Figs. 11 and 12) This feature of the Letter Serial Correlation appears on all graphs, regardless of the language, text's length, writer's style, or any other differences between the texts. On some graphs, more than one minimum was observed even after the above mentioned artifacts had been removed. An example is shown in Fig. 15a, which was shown earlier in part 3 of this article and is reproduced here again, using a larger scale.
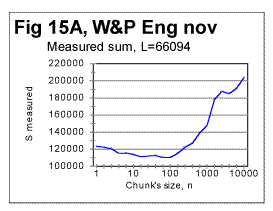
There are several minima in the above graph, at n=5, n=20, n=70. n=100, and n=5000. As it was discussed in part 3, the minima at n=5, n=70, and n=5000 were found to be caused by the text's truncation and therefore these three minima are not real characteristics of the text's properties, and have to be filtered out. However, after dismissing the above three minima, two other minima, those at n=20 and at n=100 remain and must be viewed as manifestations of the text's real intrinsic properties. Then we have to discriminate between these two real minima and determine which of them is the Primary Minimum Point, common for all texts, and which is a secondary minimum point characterizing some peculiarity of that particular text. Such discrimination can be done by comparing the text in question with other similar texts and seeing which of the two minima is evident in all similar texts, and which is a unique feature of the particular text in question. For example, for the text of Fig 15a it was determined that the minimum at n=20 is most likely the Primary Minimum Point, and therefore the minimum at n=100 is more likely a secondary one.
In this section the Primary Minimum Points (PMP) which were observed for all texts without a single exception, will be discussed. The secondary minima, which were observed for some texts, but did not appear for many other texts, will be discussed in another section.
To interpret the Primary Minimum Points, we have to answer the following questions:
1. Why at chunk's sizes n which are below that value of n=nm where PMP is observed, the increase of n is accompanied by a decrease in the measured LSC sum, Sm ?
2. Why at chunk's sizes exceeding nm, the further increase of n is accompanied by an increase of LSC sum, Sm?
3. What determines the specific locations of PMP in various types of texts?
1) The answer to question 1 can be given on two levels.
a) On the surface level, the answer seems to be rather obvious. As we have seen in part 3 of this article, as chunk's size n increases, the individual contribution of each letter to the measured LSC sum - Sm - decreases, as it is exemplified by the curves for the measured LSC density, dm vs n. It must be added that the decrease of the individual contribution of each letter to the measured LSC sum is not just a trivial decrease of a relative contribution of each letter as the total number of letters in a chunk increases. What we state is the decrease of the absolute value of the contibution of each letter, as this is what the decrease of quantity dm=Sm/n signifies.
While the above explanation leaves open the question why the individual contribution of each letter to the LSC sum decreases not only in relative, but also in absolute terms, that explanation indicates the direction of a search for a more intrinsic explanation, which seems to have to go toward clarifying how individual letters contribute to the LSC sum.
b) On a more intrinsic level, we woud need to explain the mechanism of the decreasing individual contribution of each letter to the LSC measured sum. We submit that a possible explanation of the mechanism determining the decrease of Sm as n increases from 1 to nm, was already suggested in the previous section, where it is a paragraph between signs (i) and (ii).
One more cause of the decrease of the measured sum, entailing a trivial change of the number of terms in the correlation sum as the chunk's size increases, will be dicussed in the next subsection.
2) The answer to the second question can also be suggested on two levels.
A) On a surface level, the appearance of a minimum must be a result of the superimposition of two opposite effects, at least one of them being the decreasing contribution of individual letters to the LSC sum. While this effect takes place in both randomized and meaningful texts, the opposite effect, which causes the rise of the correlation sum, manifests itself only in meaningful texts. We will discuss it a little later. While at n<nm the effect of decreasing individual contributions (plus, possibly, also some other effects acting in the same direction) , at n>nm the yet unexplained opposite effect takes over. Of course, the above explanation is actually not much more than a statement of observed facts, as it does not provide any explanation, first, what is the opposite factor, and second why these mutually opposite factors swap their relative strength at n=nm.
Let us first discuss the behavior of dm which quantity reflects the individual contribution of each letter to the LSC sum.
Let us look at Fig. 48. In that graph the results of regression analysis
are shown performed on log
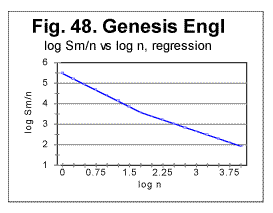
As can be seen from this graph, there are two distinctive regions, one at log n< 1.477 with a steeper slope of the sraight line representing log dm vs log n dependence, and the other at log n>1.477 with a slower, continuing decrease of log dm. The equations of these two straight lines are as follows:
At log n<1.447: log dm = 5.474-1.082log n. Correlation coefficient k=0.999969.
At log n>1,447: log dm= 4.843-0.728log n. Correlation coefficient k=0.9914.
The negative slope of the log dm vs n line decreases from 1.082 at log n<1.447 to 0.726 for log n>1.447.
Note that log 30=1.447, hence the change of the slope takes place at about n=30, which is the location where the Primary Minimum Point for that text is observed (see Table 5).
Similar data were obtained for other texts as well, indicating that the measured LSC density, which reflects the contribution of individual letters to the measured LSC sum, continuously decreases from its value at n=1, toward larger n, over the entire range of the used chunk's sizes. This decrease is faster as chunk's size grows from n=1 to n=nm where nm is the location of the Primary Minimum Point. As the chunk's size passes the location of the PMP, the LSC density continues to decrease along with the further growth of n, but measurably slower. Thus, the Primary Minimum Point is also the point where the distinctive drop in the rate of the decrease of LSC density is observed.
B) Let us discuss now the possible answer to question 2 on a more intrinsic level.
Since we have a reasonable explanation for the decrease of Sm when chunk's size n grows above n=1, the interpretation of the appearance of the minimum point would automatically follow from the interpretation of the rise of Sm at n>nm, where nm is the value of chunk's size at the Primary Minimum Point. The rise in question is absent in graphs for randomized texts, but is present in graphs for all meaningful texts, without a single exception, and, moreover, displays obvious regularities connected to the text's language and letter composition.
While it was relatively easy to offer some more or less plausible explanations for the decrease of Sm sum when n exceeds n=1, the explanation of the rise of Sm at n>nm is a much more complex task. Arguably, the rise of Sm is the most mysterious feature of the LSC effect. The decrease of the correlation sum, which is observed in randomized texts, as well as in certain ranges of chunk's size n also for meaningful texts, can be attributed to more or less trivial reasons, as those discussed so far in regard to the segment of the Sm vs n curve for n between n=1 and n=nm.
There can be suggested one more effect that causes the change of Sm value as n increases. This effect is connected with the change of the number of terms in the correlation sum as the number of chunks k changes (and correspondingly, changes the chunk's size n=L/k). Let us discuss this effect, and see if it can explain the rise of Sm sum at n>nm.
Let us consider the following situation. We conduct a test (test A) on a text divided into k1 chunks, each chunk's size being n1=L/k1. Then we decrease the number of chunks by 1, so that in test B, k2=k1-1, and the chunk's size becomes n2=L/(k1-1). In test A there are k1-1 boundaries between chunks, hence k1-1 pairs of chunks. Each pair of chunks contributes to the correlation sum a term per every letter, some of those terms possibly having zero value
In this consideration our goal is limited to estimating only how the number of terms in the correlation sum depends on the chunk's size, regardless of the values of those terms.
To understand the effect of the number of boundaries between chunks on the number of terms in the LSC sum, let us first simplify the problem by assuming that every letter appears only once in a chunk. Then the number of terms (including the zero-value terms) contributed to the LSC sum by each pair of chunks in test A is NA=(k1-1)n1. In test B the number of chunks pairs decreases by 1 and is now k2-1=k1-2. The number of terms contributed to the correlation sum in test B becomes NB= (k1-2)n2. Plugging into that formula the expressions for n1 and n2 we obtain: NA=(k1-1)L/k1 and NB=(k1-2)L/(k1-1). To compare NA and NB, we can ignore the identical quantity - L in these expressions. Then the expression characterizing the number of terms in the correlation sum in text A will be qA= (k1-1)/k1 whereas in test B the corresponding quantity is qB= (k1-2)/(k1-1). Obviously qA>qB.
The choice of k1 in this example was arbitrary. Therefore we can generalize the result we obtained for the decrease of k1 by 1, applying it also to cases when k1 decreases by any number g<k1.
In a test C, where k1 was changed to k1-g, the expression characterizing the number of terms in the correlation sum can be generalized as follows: qC=(k1-g)/(k1-g+1). Obviously for every g<k1, we have qC<qA. It means that as the number k of chunks decreases by g (and chunk's size n correspondingly increases) the net result of two simultaneous effects - decrease of the number N of terms in the correlation sum caused by decreasing k, and increase of that number caused by increasing n - is the overall slow decrease of that number N of terms. These double effect promotes the decrease of the correlation sum as n increases. This trivial effect must take place in both randomized and meaningful texts.
If chunks contain more than one appearance of each letter, the above calculation must be amended, but such an amendment would bring about only some quantitative rather than qualitative difference. The conclusion is that the increase in chunk's size (that is decrease in the number k of chunks) is accompanied by a slow decrease of the number of terms (including the zero-value terms) in the LSC sum. This effect can be partly responsible for the observed decrease of the measured sum as n increases between n=1 and n=nm.
Therefore, the effect of the change in the number of terms in the correlation sum caused by the increase in chunk's size n cannot be responsible for the increase of the measured correlation sum at n>nm. Obviously, the explanation of the rise of Sm sum at n exceeding the minimum point is not in the number of terms in the correlation sum, but in the values of those terms. More specifically, as n increases above nm, a larger fraction of terms in the sum consists of non-zero terms. It, in its turn, means that as n increases, the letter composition of chunks becomes more varied.
The rise of Sm vs n curve was never observed for randomized text. It was observed though for all meaningful texts without a single exception, for n exceeding the minimum point value. In randomized texts the superimposition of effects described earlier, such as decreased number of terms in the sum as n increases, as well as the gradually intensifying chaoticity of chunks' letter composition, invariably result in a continuous drop of the correlation sum as n increases from n=1 to the maximum value of n used. On the other hand, in all meaningful texts, there is an opposite effect. In a general way that opposite effect can be defined as gradual enhancement of variability of letter composition as chunk's size increases. This effect could hardly be foreseen but its existence is evident from all experimental data for meaningful texts.
Since the minimum point is a constant feature in all meaningful texts but is absent in all randomized texts, then the only explanation for the appearance of the minimum point, i.e. of the rise of Sm curve at n>nm must connect this effect to those peculiarities of the meaningful texts which distinguish them from randomized texts, but are common for all meaningful texts. The only feature satisfying this condition is the fact that meaningful texts possess semantic contents, which is absent in randomized texts.
It means that we have to attribute the rise of Sm vs n curve at n>nm to C-factor.
It could be rather easy to foresee that C-factor can cause local minima and other local wriggles on the curves in question, as it was illustrated earlier. However, to predict that a meaningful contents of a text would inevitably cause a regularly appearing minimum on every Sm curve, regardless of the particular semantic contents of a text, would require an inordinate feat of imagination.
Again, in randomized texts, as n increases, the occurrences of identical letters in adjacent chunks gradually become more frequent, so the sum decreases all the way from n=1 to the maximum n used.
In meaningful texts, the situation is obviously different, as the larger are chunks (at least for n>nm) the more varied is the chunks' letter composition.
3) We turn now to question 3.
The entirety of the experimental data shows that the Primary Minimum Point in all texts is located at such values of chunk's size n which are at or above n=z where z is the number of letters in the alphabet.
Indeed, in all Hebrew and Aramaic texts, except for the Samaritan version of the Book of Genesis, the Primary Minimum Point is at n=22. In the Samaritan Genesis it is at n=30. We have to take into account that our measurement for Samaritan Genesis were performed at n=10, n=20, and n=-30 but not at any points between these three locations. Therefore finding a minimum at n=30 only means that the actual minimum is somewhere between n=20 and n=50. In the case of Samaritan Genesis it is more likely between n=20 and n=30, since the Samaritan version of Genesis is in Hebrew as is the Judaic version and the difference between the two version is not very substantial from the viewpoint of letter composition. Indeed, look at Fig. 49. In that graph the measured LSC sum is shown for the Aramaic translation of the Book of Genesis (blue curve) and for its Hebrew-language Samaritan version (red curve).

It can be seen that the minimum of the red curve is at n=30 while for the blue curve it is at n=20. However, the actual minimum on both curves may be anywhere between n=20 and n=30. Hence, the seeming difference in the location of the PMP in the Samaritan version (at n=30) and in all other Hebrew and Aramaic texts (at n=22) very likely is not real, as in all cases in question, the actual minimum is somewhere between n=20 and n=30. Recall now that the number of letters in Hebrew alphabet is z=22. The natural assumption is that the Primary Minimum Point's location is associated with the number of letters in the alphabet, thus being largely determined by A-factor.
Turn now to English and Russian texts. Since the number of letters in the English alphabet is z=26, and in the Russian alphabet it is z=33, while the closest values of n for which the measurements were performed are n=30, and n=50, it seems reasonable to expect that the Primary Minimum Point in English and Russian texts would be found close to n=30. Indeed, it turns out to be true for many English and Russian texts studied, such as the English translation of Genesis, Macbeth, The Song of Hiawatha, Short Stories both in Russian and in English (Table 5). Then, if an English text is stripped of vowels, the alphabet in use shrinks from 26 to 21 letters, and when it is stripped of consonants, the alphabet in use shrinks to only 6 letters. For Russian alphabet the corresponding values are 24 and 8. Hence, it seems reasonable to assume that for English and Russian texts stripped of vowels, the Primary Minimum Point's location would shift to be close to n=20, and for texts stripped of consonants, it would shift to be close to n=5 or n=10. Indeed, that is what was observed in many texts treated that way, such as Macbeth, Hiawatha, Short Stories both in English and Russian. In all those cases the PMP in the texts stripped of vowels was found at n=20, while in the texts stripped of consonants it was found at n=10 (Table 5).
Regarding the mechanism responsible for the A-factors' effect on PMP's location, it had actually been already discussed in relation to the Downcross point (a paragraph between signs i and ii). As it was suggested in that explanation, as long as the chunk's size n is less than the number z of letters in the alphabet, not every letter of the alphabet can find a space in a chunk. This imposes a restraint on the composition of the measured LSC sum. In the paragraph included between signs i and ii, the mechanism of that restraint was suggested. At n=z (or at some n higher than z) when all letters of the alphabet acquire a chance to be in a chunk, the restraint is lifted.
Whereas in no texts was the PMP location found to be at n<z , there are some texts where PMP location was found at n>>z. For example, in the text of the UN convention on the Sea, the Primary Minimum Point happens at n=85, which is almost three times the number of letters in the alphabet. In the text of the English translation of War and Peace, PMP was found at n=70, and in some segments of War and Peace and in the text of Moby Dick it was at n=50. Likewise, in the text of the Russian newspaper, PMP was at about n=40.
In all these text, when they were stripped of vowels, and even more when stripped of consonants, the PMP shifted considerably toward smaller n, as it was also the case with all other texts. For example, in Moby Dick stripped of vowels, PMP location shifted from n=50 to n=30, and when stripped of consonants, it shifted to n=10. In UN convention, the shifts were to n=75 and n=20. In the Russian newspaper, when stripped of vowels, PMP moved from n=50 to n=20. (See Table 5). Hence, while the general trend is the same in all texts, in some of them, such as Moby Dick, UN convention, and the Russian newspaper, the values of n for PMP are typically above z, which is the number of letters in the alphabet.
Considering the collection of texts where PMP is at n>>z, we can notice that all these texts have one thing in common. Without applying any quantitative measure, we have a distinctive feeling that, for example, the UN convention is written in a heavy "Legalese," with long convoluted sentences and with a wide use of long Latin words rather than of shorter Anglo-Saxon ones. Also, both War and< Peace and Moby Dick are known for verbosity. The text of the Russian newspaper is writen in a "Journalese." All these styles are quite distinctive from the poetic brevity of Hiawatha or Macbeth or of the rather laconic style of Short Stories.
Here is a corollary to the above statement. It seems reasonable to assume that the texts written in "Legalese" or "Journalese" make a wider use of longer words. Hence the average lengths of words in a text may serve as some characteristic feature of a text from the viewpoint of its style. Namely, the "heavier" is the text's style, the larger is the average length of words in that text. The average length of words in a text can be estimated by dividing the total number of letters in a text by the total number of words in that text. The results of such an estimate are rather instructive. Here are a few examples. The average word length in the Russian newspaper is 5.84 letters. In the text of Short Stories in Russian it is only 3.67 letters per word, while in the English version of the Short Stories it is 3.39 letters per word. In the text of The Song of Hiawatha (where a number of rather long native Indian names is scattered all over the text) it is 4.8 letters per word, which is still substantially less than in the newspaper. Even though the average words' length is not a very precise measure of texts' behavior, the mentioned examples jibe well with the above hypothesis in regard to the reason for several English and Russian texts to have the PMP at nm>>z, unlike the texts written in a more succinct style whose PMP are found close to nm=z. Hence, it seems reasonable to attribute the relatively high value of nm in some of the studied text to C-factor, if we interpret that factor as encompassing not only the subject of the contents but also its style.
We submit that A-factor determines the lower threshold for the location of PMP. At n<z the appearance of PMP is prohibited by A-factor (which does not prevent the appearance of secondary minima at n<z). As the chunk's size reaches the value of n=z, the constraints imposed by A-factor are lifted and the occurrance of the PMP becomes possible. However, other factors, most notably C-factor, and possibly also V-factor, may prevent the appearance of PMP until some higher value of n. Possible mechanisms of C-factor's and of V-factor's effects were discussed earlier.
The upcross point nu is where the curves for the measured sum Sm (as it is sloping up) and for the expected sum Se (as it is sloping down) intersect. Recall that Sm and Se> are defined in different ways. The measured sum is found by measuring its terms directly on an actual text. The expected sum is calculated assuming that the text is the average of all versions of that text randomized by permutation. Both sums are found for the same text's length and the same letter frequencies distributions. Otherwise, though, they are found for two different texts, one the real, particular meaningful text, and the other is calculated for a hypothetical averaged randomized text of the same length and with the same letter frequency distribution. Speaking metaphorically, these two sums have no knowledge of the behavior of each other. Each of the two curves, one for Se vs n and the other for Sm vs n dependencies, runs its own way, being not aware of the existence of the other curve. Somewhere on their paths these two curves intersect. For neither of these two curves is the intersection point in any sense its own characteristic point. On the other hand, the location of the Upcross point (UCP) seems to occur in a rather regular fashion, consistently appearing at chunk's sizes which are typical of particular languages and alphabets.
Indeed, in the Hebrew texts, the UCP invariably occurs at chunk's sizes nu which are substantially lower than those for English texts (Table 5). While for Hebrew and Aramaic texts the UCP is consistently observed at n=85-150, for the majority of the all-letter English texts it is often at nu=400-800, although in some all-letter English texts (for example in Hiawatha) it happens at nu=150. In Russian texts the location of UCP was observed at n=350 for the newspaper and at n=250 in Short Stories. The general trend is that for the texts with a higher value of nm - the location of the Primary Minimum Point - also UCP is observed at higher nu , which is a simple, purely geometric fact, as the more nm shifts to the left, the farther moves to the left also the intersection of Sm vs n curve with Se vs n curve. In the English and Russian texts stripped of vowels, and even more in texts stripped of consonants, UCP shifts towards lower values of n, approaching those for Hebrew texts.
Simple geometric considerations indicate that besides the location of the Primary Minimum Point, the intersection of curves for Sm and Se must depend on the slopes of both curves - the slope down for Se and the slope up for Sm . The steeper rises Sm as n increases above nm, and the steeper drops Se as n increases above nm, the sooner they intersect. This is illustrated in Figs. 50 through 53.

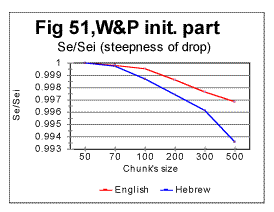
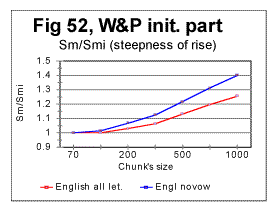
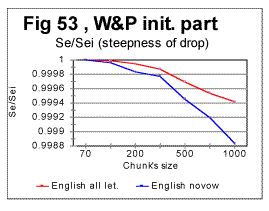
In the above four graphs, the ratios Rsm=Sm/Smi and Rse= Se/Sei are plotted versus the chunk's size n, for the range of n between the Primary Miminum Point -nm - and an arbitrarily chosen point at some n slightly larger than nu - the Upcross point. In these two ratios, Smi and Sei are the values of the measured - Sm, and the expected - Se, sums at n=nm, i.e. at the Primary Minimum Point. Hence, all these curves start at n=nm where the ratios' values are both 1. The curve for Rsm shows how steep is the rise of Sm between the PMP and Upcross point, while the curve for Rse shows how steep is the decrease of Se in the same range of n. The steeper is the rise of Sm or the drop of Se, the sooner the curves for these two sums intersect, and hence the lower is the value of nu - the Upcross point. As only relative values are used, the possible effect of different text's size has been eliminated in these graphs. In Fig 50 the comparison is made between the rates of rise of Sm for the all-letter English translation of the initial part of War and Peace, 107100 letters long (red curve) and the same portion of the Hebrew translation of that text (blue curve). In Fig. 51 the rates of Se decrease are compared for the same two texts, red curve for the English and blue curve for the Hebrew version. In Fig 52 and 53 a similar comparison is made between the same portion of War and Peace as in Fig. 50, as an all-letter version (red curves) and the same text stripped of vowels (blue curves). As it can be seen in these graphs, switching from the English to the Hebrew version of the same text results in a larger steepness of both Sm's rise and Se's drop, and therefore the curves for both sums necessarily intersect at lower n in a Hebrew text than they do in the English one. Likewise, stripping the text of vowels results again in the larger steepness of both Sm's rise and Se's drop, again ensuring the shift of the Upcross point toward lower n.
The described effect seems to be a little more pronounced for the expected sum than for the measured one, but both sums' behaviors contribute comparably to the described shift of nu to lower values.
The described effect takes place in a quite consistent fashion, invariably following the difference in the alphabets' sizes (Table 5). Therefore it seems reasonable to attribute the shift of the Upcross location to A-factor, even though this is most likely just a side effect, as the Upcross point is simply the incident of intersection of two curves actually independent of each other. The behavior of both Sm vs n and Se vs n curves in general, and their slopes in particular are determined by the changes in the texts' structure. If a text uses a smaller alphabet, the number of terms in both the measured and the expected sum decreases, which leads to the overall shift of all characteristic points toward smaller values of chunk's size n. The smaller is the number of letters in the alphabet, the less of a text's length it takes to complete any change in the text's structure. Therefore the slopes of both curves are steeper in the texts with a smaller number z of letters available for the text.
d. Peak points
The values of chunk's size np where peaks are observed on a Sm vs n curve are gathered in Table 6. If in the cell for a particular text inTable 6 there is phrase "n/observ." it means that in the range of chunk's sizes n between n=1, and the maximum chunk's size used for this text, no peak was observed, while it is possible a peak would be seen if the chunk's size were expanded (if the overall text's length L allowed such an expansion of the chunk's maximum size). The lengths L of the texts are listed in Table 4, and the maximum sizes of the chunks for the texts are listed in Table 5.
While discussing the peaks on Sm vs n curves, we have to account for the following facts:
1. Peaks are observed not for all texts.
2. If peaks show up for a text, it is usually at rather large values np of chunk's size (see Table 6).
3. The texts that show no Peak Points, all are relatively short (mostly L<150000).
4. In a few cases peaks were observed at values of n substantially lower than for the majority of peaks. These were peaks in the English translation of Genesis at np=3000, in its no-vowels version at np=7000 and in the Hebrew original of Genesis at np=7000. If we postulate that these few exceptional peaks that appear at relatively low values of chunk's size n are caused by a factor different from the rest of the peaks (and we assume that this different factor is what we denoted C-factor. i.e these peaks are caused by local peculiarities of the text's contents) then for the rest of the texts there seem to be a certain correlation between np -Peak Point location, and the values of Dr - the coefficient we named Degree of Randomness. Namely, the overall trend seems to be that large values of np correlate with lower values of Dr (Table 6). Degree of Randomness will be discussed in the next section, but we can recall now that this coefficient was introduced as a rough cumulative measure of the overall closeness of the text in question to a randomized text.
5. The expected sum Se which is calculated for an averaged randomized text, decreases rather evenly all over the range of chunks' size n. In the absence of text's truncation, the curve for Se would be a straight line dropping to zero at n=L, where L is the total length of the text. Because of text's truncation at some values of chunk's size n, the Se vs n curve becomes actually a partial (open) polygon dropping toward zero as n increases.
6. In the text where an artificial long range order was created by adding repeatedly the same segment to the text, the Peak Point is observed at the chunk's size that is equal to the length of the repeatedly added segment: n=m.
To account for all six listed observations, the following interpretation seems to be plausible.
Recall that in the section dealing with the texts of variable length we found that the studied texts, first, possess a rather high degree of a short range order, and also some degree of an imperfect long range order.
The short range order extends only over segments of texts comprising a certain topic, or theme, and as soon as that topic or theme is done with, the short range order is broken. The length of the segment which covers a certain topic, may vary in a rather wide range, from a few hundreds to many thousands of letters. It seems though plausible to assume that the short range order does not extend over segments comprising tens of thousands of letters. As one topic is replaced with another at some value of n, the Sm vs n curve may react with a wriggle, such as local minimum, or a local peak. We submit that this is the probable source of peaks at relatively low np as it is the case in Genesis. We denoted this mechanism as C-factor.
The long range order may extend over much larger segments of texts, and must be closely connected to the Letter Serial Correlation effect. As chunk's size increases, each chunk encompasses larger segments of text. Since the long range order in the studied texts is imperfect, it means the texts contains certain clusters of letters which do not conform to the overall pattern of the long range order. They act as defects diluting the long range order. With the increase in text's lengths, the described dilution gradually accumulates. At a certain text' length, Lc , the accumulation of defects results in a critical deterioration of the long range order. In other words, at a certain chunk's size np, which is expected to be in the range of at least thousands, and more probably tens or even hundreds of thousands of letters, the long range order breaks down. Starting at this chunk's size, the text behaves more like a random than like an ordered text. This interpretation seems to be plausible also from the viewpoint of the simple common sense. If the text that is L letters long is divided into hundreds or thousands of small chunks, the distribution of letters within those chunks, which depends on the particular contents of the text in various parts of the entire text, can vary substantially from chunk to chunk. However, if the text that is 1 million letters long, is divided into two segments 500000 letters each, the large size of each chunks causes leveling off of the local variations in the letter distribution, so that the overall character of the text approaches that for the random one.
Here we encounter a seemingly paradoxical situation. The perfect long range order (as we created it artificially by adding repeatedly the same segment of text) results invariably in the LSC sum dropping to zero as soon as chunk's size n=m where m is the size of the repeatedly added segment. The absence of a substantial degree of order, i.e. randomization of a text, also results in the LSC sum dropping to zero at a sufficiently large n (which in the absence of the text's truncation would be at n=L). Hence, both the perfect order and the nearly complete disorder ultimately result in the same, namely zero value of LSC sum. The difference is in that the perfect order causes the sum to drop to zero, first, abruptly, and, second, inevitably, while the nearly complete disorder causes a drop of the sum to zero which is, first, gradual, and, second, this outcome is just the most probable one rather than inevitable. However, the probability of the said outcome is so overwhelming that the second difference is of no practical consequence.
To summarize the interpretation of Peak Points, we submit that the Peak Points appear at such values of chunk' size np where the long range order has completely deteriorated. Hence, if some texts (Table 6) show no Peak Point it means the text in question is just too short and does not reach the value of Lc necessary to lose the long range order. After passing the Peak Point, that is at n>np the text behaves more like a random one, so now the LSC sum decreases as it is typical of randomized texts. The reasons for the LSC sum in random texts to decrease as n grows were discussed earlier.
The values of Degree of Randomness introduced in part 2 are shown for all studied texts in the second from right column of Table 6. Recall that Dr is a cumulative measure roughly estimating the closeness of the ratio R= Sm/Se to its value for an averaged randomized text. Recall also that for all actual texts randomized via permutations of meaningful texts, both in English and in Hebrew, the values of Dr turned out to be above 0.9, while, as can be seen from Table 6, the values of Dr for all meaningful texts, regardless of the language, text's length etc, all are substantially lower than 0.9, thus justifying the use of Dr as a rough measure of degree of randomness.
The following features of Dr behavior are to be mentioned:
1. The values of Dr for the texts in Hebrew and Aramaic are consistently lower than they are for English and Russian texts. For example, for the Hebrew text of the Book of Genesis Dr= 0.2 , while for the English translation of the same text Dr= 0.3. Typically, in Hebrew and Aramaic texts Dr was found to be below 0.3, while in English and Russian texts it is often above 0.5. Relatively low values of Dr were found for the UN convention with its rigid structure of "Legalese."
2. Stripping English or Russian texts of vowels or consonants does not result in a consistent drop in Dr value. For example, for the all-letter text of Short Stories in Russian Dr=0.319, but for the same text stripped of vowels it increased to Dr=0.517 despite the decrease in the number of letters used. On the other hand, for the all-letter text of the Russian newspaper Dr=0.632, and for the same text stripped of vowels it decreased to Dr=0.577. Similar variations of Dr were found for other texts (Table 6).
3. The value of Dr does not seem to consistently change depending on the text's length, as can be seen by comparing the values of Dr in Table 6 with the corresponding texts' lengths given in Table 4.
The listed observations seem to indicate that the value of Dr is not affected substantially by A-factor, i.e. by the number of letters in the alphabet. Since Dr is an aggregate measure for the entire text, neither must it depend on the local variations in contents, i.e. on C-factor. Then the behavior of Dr supposedly must depend on the two remaining factors we postulated, namely G-factor and V-factor, the first representing the role of the language's Grammar structure and the second, the vocabulary available in a language. V-factor seems to be a better candidate to explain the behavior of Dr. The vocabulary factor determines the scope of variations of words used in a particular language to convey the same "amount of contents." Since the Hebrew and Aramaic vocabularies are substantially more limited than the Russian or English, identical words, and hence identical sets of letters, happen in Hebrew and Aramaic texts more often. So, in Hebrew/Aramaic texts there is less freedom of choice of letters as one proceeds along the text. Metaphorically, it can be expressed as fewer degrees of freedom in Hebrew and Aramaic texts as compared with English or Russian texts. Coefficient Dr senses it as if this is the diminished randomness of Hebrew/Aramaic texts as compared with English or Russian texts (of course, actually the situation is the opposite one). We submit therefore that the behavior of Degree of Randomness - Dr - mainly reflects the V-factor. It does not mean that other factors, both listed as A, G, and C, and those not listed but also possibly existing, cannot have a role in Dr's behavior.
f. Secondary minima, crossover points, and peaks.
As it was mentioned earlier, besides the regular features such as Downcross point, Primary Minimum Point, Upcross point, (and now we add to the regular features Peak Point as well) there are on some Sm vs n curves additional peculiarities in the form of secondary (and sometimes tertiary) minima, crossovers with Se vs n curve, and peaks, which remain after the artifacts caused by the text's truncation have been filtered out. These secondary characteristic points appear without forming a consistent pattern. Therefore the only reasonable explanation for the presence of those secondary irregularities is to attribute them to C-factor, i.e. to the particular semantic contents of the local portion of the text. An example showing how such particular contents of a paragraph can cause a sharp wriggle on the measured LSC sum curve, was discussed earlier.
6.Conclusion
It has been shown in this work that meaningful texts, exemplified by a number of texts in English, Russian, Hebrew, and Aramaic, are characterized by the presence of a complex ordered structure distinguishing these texts from randomized collections of symbols (and, by extension, even more from perfectly random texts). One manifestation of that complex order is the Letter Serial Correlation effect which had been studied in this work in a considerable detail.
The results reported in the four parts of this paper are obviously just a first step toward the more comprehensive study of different forms of order in written languages.
We can contemplate a number of directions for the continuation of that study, to wit:
1. To study more languages. While the four languages subjected to the study belong to three different groups of languages (Semitic, Germanic, and Slavic) there are many languages differing very substantially from all three mentioned groups. From this viewpoint, it would be interesting to include into possible further study, for example, such languages as Finnish, Polynesian, Chinese, and also languages of some tribes in Africa, Australia, and South America. (The results of the LSC tests conducted in some other languages will be posted soon in this page).
2. To study effects other than LSC. There are in the languages many forms of order, with multilayered overlapping correlations. Studying these effects may shed light on the mystery of that miraculous means of communication which is a written language.
3. To study encrypted texts. Revealing the behavior of LSC and of other forms of order in encrypted texts may be useful for deciphering ancient inscriptions and manuscripts written in unknown languages. We made a very preliminary effort in this direction, but the resuts have so far been too inconclusive to be reported .
4. To study patterns of order formed by ELS (Equidistant Letter Sequences) as well as by GISLS (Gradually Increasing Skip Letter Sequences) and GDSLS (Gradually Decreasing Skip Letter Sequences). Such study might substantiate arguments either in favor or against the still surviving hypothesis about the so called "codes" in the scriptures.
The list of possible directions of the further study can be expanded and this seems to present a challenge to aspiring researchers. The authors of this paper are not linguists and have their own areas of interest and training, and would be happy to relay the subject to any enthusiastic replacement crew.
Even though we have reported in this paper on the tests conducted only in four languages, it seems to be possible to offer one general conclusion, and here it is.
We have considered in this paper texts which varied in length, topic, writer's style, and, most important, languages and historical eras when these texts had been written. There are certain quantitative differences between texts, which are due to the language used, to the text's topic, style, etc. However, what seems to be more amazing, is the striking qualitative similarities between all texts explored. The texts written in Hebrew thousands years ago, behave in many respects exactly like the texts written in English in the 20th century. The text of a contemporary newspaper printed in Russian in Moscow, and the text of an English or Hebrew translation of Tolstoy's masterpiece, display amazingly similar characteristics, which however are absent in the texts randomized by letters permutations. Text of Talmud, written in two languages, Hebrew and Aramaic, many centuries ago, obviously possesses the same principal types of order as does a combination of contemporary short stories written partly in Russian and partly in English, and then converted, via double translation, into two analogous texts, one fully in English and the other fully in Russian. A poem by an American poet of 19th century, and Shakespeare's famous tragedy display the same principal types of ordered structure, etc, etc.
It looks as if we can say that actually we all, Russian, Israelis, Americans, and possibly also Japanese, Hawaiians, Canadian Eskimos, etc, speak the same language, even though we do not realize it. The languages differ in Grammar, vocabulary, accents, figures of speech, etc, etc.... But somewhere on a deeper level, it all is the same language, obeying the same ground rules, varying on the surface, but stemming from the same roots, and built up following the same fundamental guidelines. The difference between languages is only on some skin-thin level, under which there is the same structural foundation. It ties together all languages as being just variations of coats, of which there is a multitude, while the body under it is the same for all of us.
Comment: In separate papers, to be posted soon, the application of the LSC test to the analysis of the mysterious medieval text known as Voynich manuscript, as well as the tests of the LSC effect in eight more languages, will be reported.
We would like to end our discourse with the following facetious lines:
HAIL THE LSC!
The Serial correlation
Is a funny, nice effect,
The same for every nation,
Each creed and every sect.
There are distinctive minima
On curves for LSC,
As clear as in a cinema
Is a film for all to see.
The curves have the propensity
To hide behind veneer,
So when you plot the density
Those minima disappear.
Of course, you may be curious:
What is its use for us?
So what, if still obscure is it
Concealed from human eyes?
And you are right - it's just a toy....
But think of a home run.
You cannot eat it, but enjoy
It, having lots of fun.
And LSC can't kill or maim
And proves for all to see
That human tongues are all the same.
So hail the LSC!
Originally posted to Mark Perakh's website on February 9, 1999.
Comments: marperak@cox.net or bdm@cs.anu.edu.au
